StanでFused LASSOしてみたかった

テストデータ
genlassoパッケージによる実装
正則化項による実装
状態空間モデルで実装
コメント

StanでLASSOを実装すると、罰則化項Lambdaも同時に最適化できる。

そりゃいいなと思ったのでFused LASSOも実装してみたくなった。

Fused LASSOは隣合う回帰係数の差が疎であると仮定するもの。

ステップ状の時系列データのデノイズなんかに使える。

LASSOにおける罰則項は回帰係数\(β\)のL1ノルム\(\sum_i{|\beta_i|}\)だったところを、 Fused LASSOでは隣合う回帰係数の差のL1ノルムに書き換えれば良い\(\sum_i{|\beta_{i+1} - \beta_{i}|}\)。

しかし、現状、どうにもうまくいってません……。

テストデータ

set.seed(1)
df <- data.frame(
  Y_true = c(rep(0, 20), rep(2, 20), rep(0, 20))
) |>
  dplyr::mutate(
    Y = Y_true + rnorm(dplyr::n(), 0, 0.2),
    T = seq(dplyr::n())
  )

g <- ggplot2::ggplot(df) +
  ggplot2::geom_line(ggplot2::aes(T, Y_true)) +
  ggplot2::geom_point(ggplot2::aes(T, Y))
g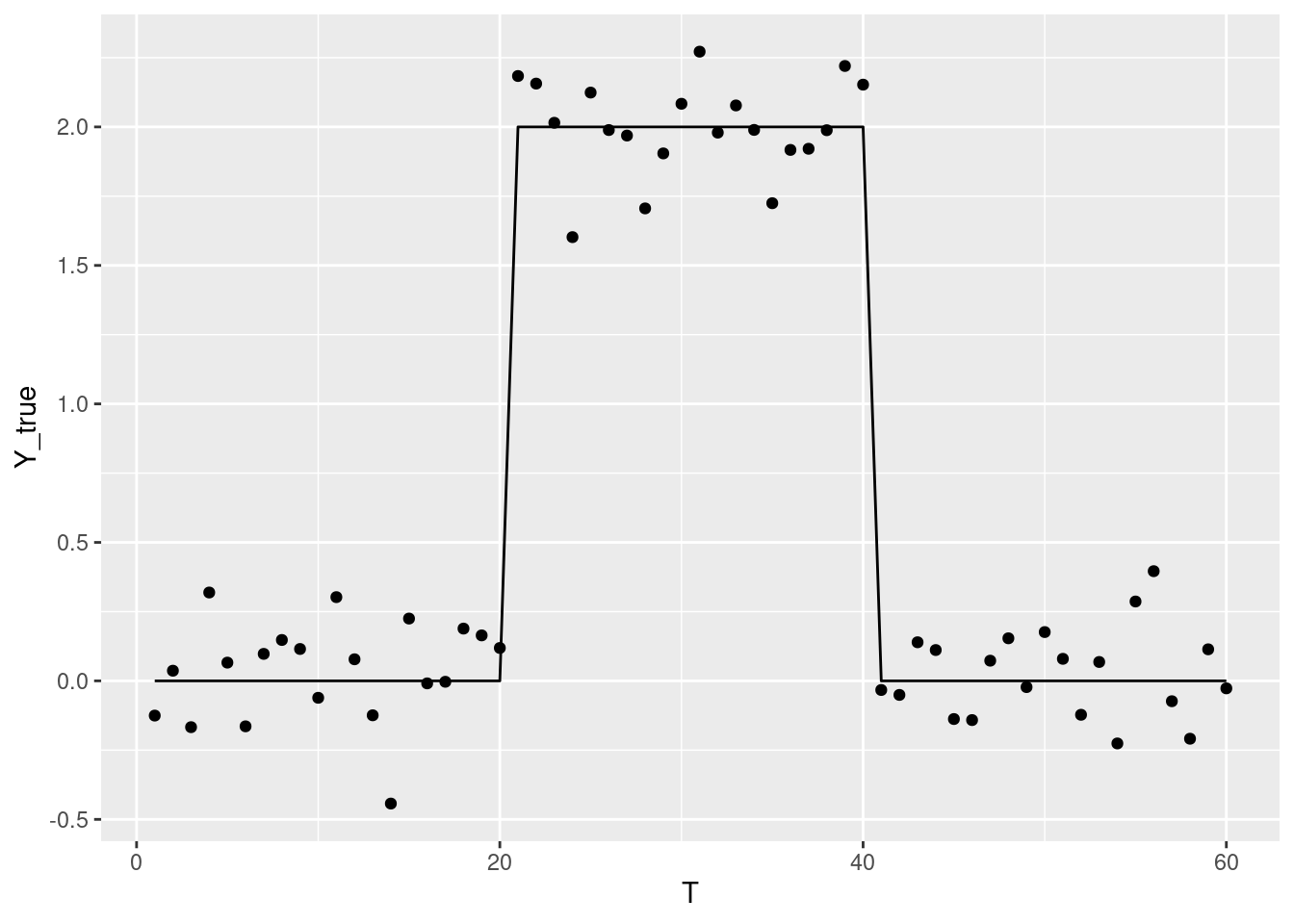

genlassoパッケージによる実装

めっちゃ簡単です。

fused <- genlasso::fusedlasso1d(df$Y)

結果を表示すると、Lambdaを大きくするほどノイズを無視してステップ状になります。

Lambdaを大きくしすぎると、本来のステップからずれた位置に推定されたステップが現れる点に注意。

十分に大きくすると、ただの水平線になります。

# 時刻T、Lambda、回帰係数βから成るデータフレーム
beta <- as.data.frame(fused$beta) |>
  setNames(fused$lambda) |>
  dplyr::mutate(T = dplyr::row_number()) |>
  tidyr::pivot_longer(
    cols = -T,
    names_to = "lambda",
    values_to = "beta",
    names_transform = list(lambda = as.numeric)
  )

# データフレームbetaの内、一部を表示
g +
  ggplot2::geom_line(
    ggplot2::aes(x = T, y = beta, color = lambda, group = lambda),
    data = beta |> dplyr::filter(0.2 < lambda & lambda < 5)
  ) +
  ggplot2::scale_color_viridis_c()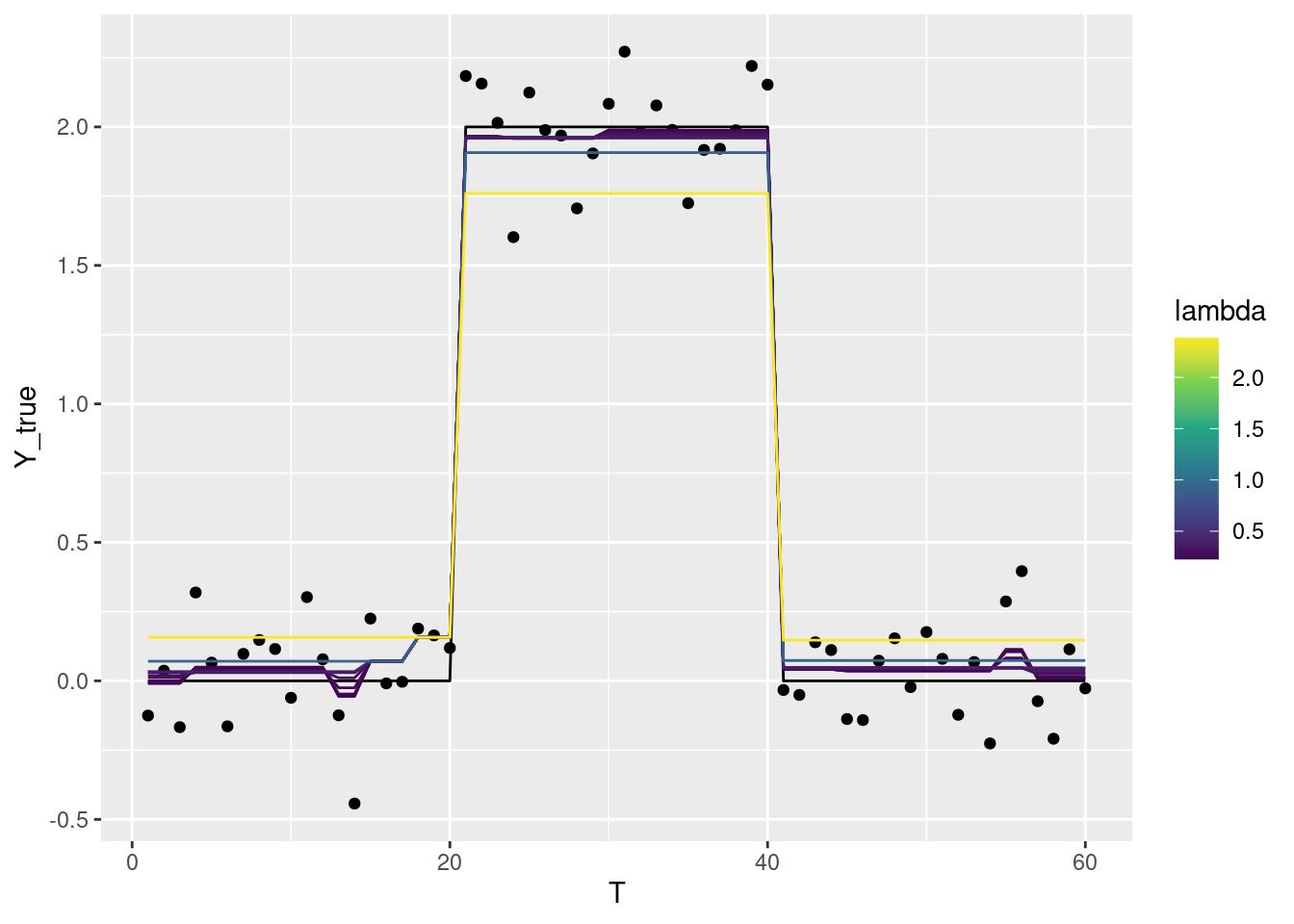

正則化項による実装

StatModeling MemorandumさんのStanによるLASSO実装を参考に、罰則項を\(\sum_i{|\beta_i|}\)から\(\sum_i{|\beta_{i+1} - \beta_{i}|}\)に置き換えます。

https://statmodeling.hatenablog.com/entry/bayesian-lasso

// fused1.stan
data {
   int<lower=1> T;
   matrix[T,T] X;
   vector[T] Y;
   real<lower=0> Lambda;
}
parameters {
   vector[T] beta;
}
transformed parameters {
  vector[T-1] beta_d1;
  real<lower=0> squared_error;
  beta_d1 = beta[1:T-1] - beta[2:T];
  squared_error = dot_self(Y - X * beta);
}
model {
  target += -squared_error;
  for (k in 1:(T-1))
    target += -Lambda * fabs(beta_d1[k]);
}

ではサンプリングしてみましょう。

genlassoパッケージの結果を参考に今回はLambda = 2を試してみましょう。

ちなみにLambdaをparametersブロックで定義すれば、同時に探索できますが、どうにも0.019とか低い値がMAP推定になります。

## Warning in readLines(file, warn = TRUE): incomplete final line found on '/home/
## rstudio/Documents/github/atusy/blog/content/post/2022-01-12-stan-fused-lasso/
## fused1.stan'

## Trying to compile a simple C file

## Running /usr/local/lib/R/bin/R CMD SHLIB foo.c
## gcc -I"/usr/local/lib/R/include" -DNDEBUG   -I"/usr/local/lib/R/site-library/Rcpp/include/"  -I"/usr/local/lib/R/site-library/RcppEigen/include/"  -I"/usr/local/lib/R/site-library/RcppEigen/include/unsupported"  -I"/usr/local/lib/R/site-library/BH/include" -I"/usr/local/lib/R/site-library/StanHeaders/include/src/"  -I"/usr/local/lib/R/site-library/StanHeaders/include/"  -I"/usr/local/lib/R/site-library/RcppParallel/include/"  -I"/usr/local/lib/R/site-library/rstan/include" -DEIGEN_NO_DEBUG  -DBOOST_DISABLE_ASSERTS  -DBOOST_PENDING_INTEGER_LOG2_HPP  -DSTAN_THREADS  -DBOOST_NO_AUTO_PTR  -include '/usr/local/lib/R/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp'  -D_REENTRANT -DRCPP_PARALLEL_USE_TBB=1   -I/usr/local/include   -fpic  -g -O2 -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -g  -c foo.c -o foo.o
## In file included from /usr/local/lib/R/site-library/RcppEigen/include/Eigen/Core:88,
##                  from /usr/local/lib/R/site-library/RcppEigen/include/Eigen/Dense:1,
##                  from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:13,
##                  from <command-line>:
## /usr/local/lib/R/site-library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:1: error: unknown type name ‘namespace’
##   628 | namespace Eigen {
##       | ^~~~~~~~~
## /usr/local/lib/R/site-library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:17: error: expected ‘=’, ‘,’, ‘;’, ‘asm’ or ‘__attribute__’ before ‘{’ token
##   628 | namespace Eigen {
##       |                 ^
## In file included from /usr/local/lib/R/site-library/RcppEigen/include/Eigen/Dense:1,
##                  from /usr/local/lib/R/site-library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:13,
##                  from <command-line>:
## /usr/local/lib/R/site-library/RcppEigen/include/Eigen/Core:96:10: fatal error: complex: No such file or directory
##    96 | #include <complex>
##       |          ^~~~~~~~~
## compilation terminated.
## make: *** [/usr/local/lib/R/etc/Makeconf:168: foo.o] Error 1
## 
## SAMPLING FOR MODEL 'fused1' NOW (CHAIN 1).
## Chain 1: 
## Chain 1: Gradient evaluation took 3.2e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.32 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1: 
## Chain 1: 
## Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 1: 
## Chain 1:  Elapsed Time: 1.26572 seconds (Warm-up)
## Chain 1:                1.14948 seconds (Sampling)
## Chain 1:                2.4152 seconds (Total)
## Chain 1: 
## 
## SAMPLING FOR MODEL 'fused1' NOW (CHAIN 2).
## Chain 2: 
## Chain 2: Gradient evaluation took 5.6e-05 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.56 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2: 
## Chain 2: 
## Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 2: 
## Chain 2:  Elapsed Time: 1.1476 seconds (Warm-up)
## Chain 2:                1.08013 seconds (Sampling)
## Chain 2:                2.22773 seconds (Total)
## Chain 2: 
## 
## SAMPLING FOR MODEL 'fused1' NOW (CHAIN 3).
## Chain 3: 
## Chain 3: Gradient evaluation took 2e-05 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.2 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3: 
## Chain 3: 
## Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 3: 
## Chain 3:  Elapsed Time: 1.31638 seconds (Warm-up)
## Chain 3:                1.13865 seconds (Sampling)
## Chain 3:                2.45504 seconds (Total)
## Chain 3: 
## 
## SAMPLING FOR MODEL 'fused1' NOW (CHAIN 4).
## Chain 4: 
## Chain 4: Gradient evaluation took 1.8e-05 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.18 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4: 
## Chain 4: 
## Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 4: 
## Chain 4:  Elapsed Time: 1.17579 seconds (Warm-up)
## Chain 4:                1.08785 seconds (Sampling)
## Chain 4:                2.26363 seconds (Total)
## Chain 4:

では可視化。むむむ。

df_pred <- data.frame(Y = colMeans(rstan::extract(fit1, "beta")[[1L]])) |>
  dplyr::mutate(T = dplyr::row_number())
g +
  ggplot2::geom_point(ggplot2::aes(x = T, y = Y), data = df_pred, color='red')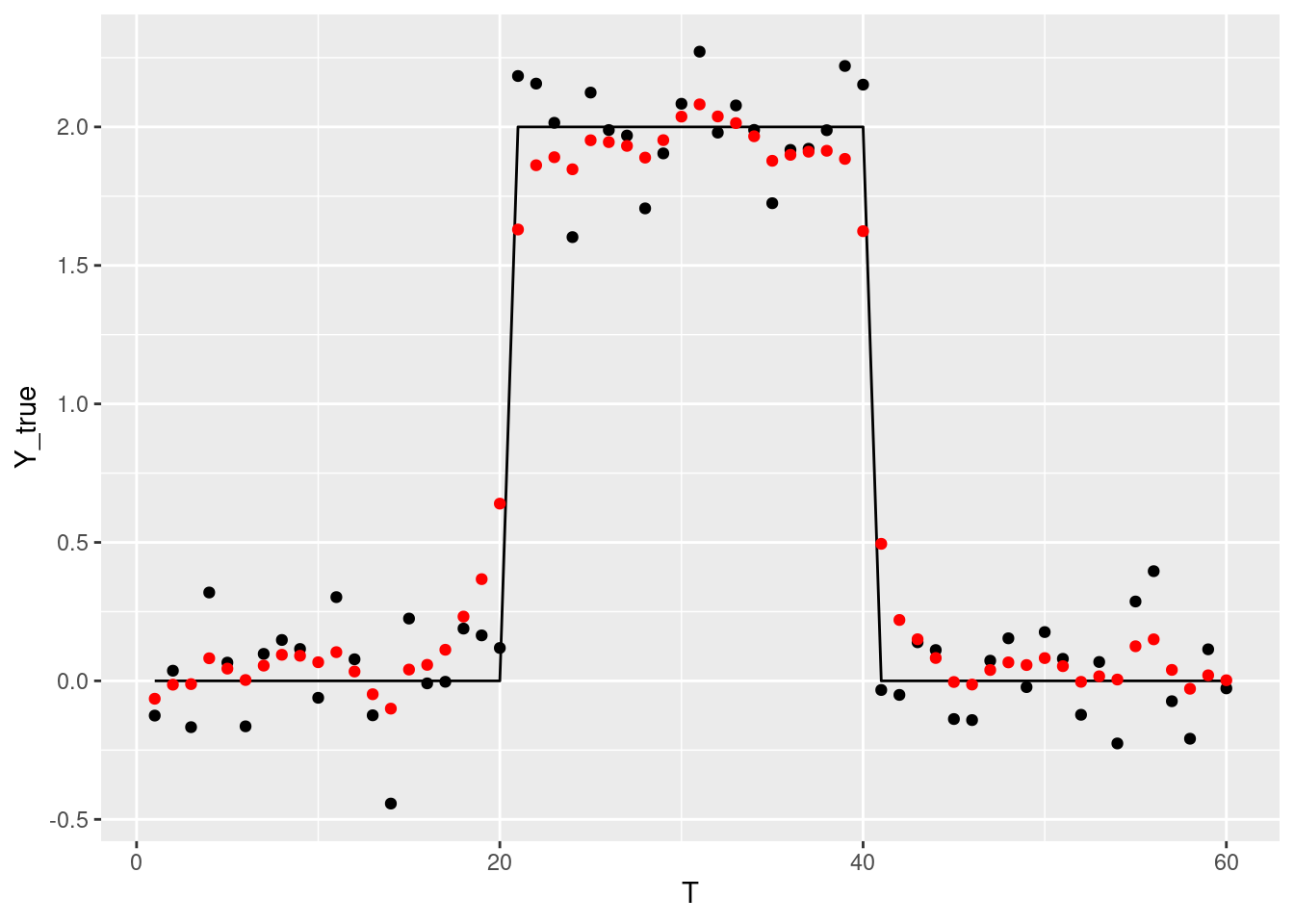

状態空間モデルで実装

たぶん、隣合う係数の差がdouble_exponential(0, s_mu)に従うと記述すればOK。

でもうまくいかない。

罰則化項で実装した時もLambdaをサンプリングするとMAP推定が低くなりすぎたので、同じ問題を抱えてそう。

data {
  int T;
  int T_pred;
  vector[T] Y;
}

parameters {
  vector[T] mu;
  real<lower=0> s_mu;
  real<lower=0> s_Y;
}

transformed parameters {
  vector[T-1] mu_d1;
  mu_d1 = mu[1:(T-1)] - mu[2:T];
}

model {
  mu_d1 ~ double_exponential(0, s_mu);
  // ↓を↑に書き換えた
  // mu_d1 ~ normal(0, s_mu);
  Y ~ normal(mu, s_Y);
}

generated quantities {
  vector[T+T_pred] mu_all;
  vector[T_pred] y_pred;
  mu_all[1:T] = mu;
  for (t in 1:T_pred) {
    mu_all[T+t] = normal_rng(mu_all[T+t-1], s_mu);
    y_pred[t] = normal_rng(mu_all[T+t], s_Y);
  }
}

むずい……。

変化点検出したいだけなら、double_exponentialじゃなくてcauchy使うのがよさそうな感じしますねー。

その時に収束しやすくする方法は「StanとRでベイズ統計モデリング」を参考にしてください。

テストデータ

genlassoパッケージによる実装

正則化項による実装

状態空間モデルで実装

コメント