欠損値の発生過程の類別

by
カテゴリ:
タグ:

先日、欠損値の発生過程の例を図示してTweetしたところ、思ったより反響がよかったので、図をブラシュアップの上、記事に残すことにした。

俄仕込みなので、間違いがあったらTwitterで指摘して下さい。

欠損値の発生過程は大きく3種あるとされる。

理解においてはMCAR, MAR, MNARの字面をあまり追い過ぎないのがキモだと思う。「ある変数」を「データ」と記載する例も見かけるが、前者の方が個人的には分かりよい。また、ランダムという言葉に惑わされがちだが、ここでのランダムはモデルとしてランダムか、ではなく、観測者にとってランダムに見えるか、くらいの気持ちでいた方がいい。

それでは欠損したデータを人工的に作って図にしてみよう。

xとyが平均0、分散1の正規分布に従う変数で、xの一部が欠損しうるとする。

そのとき、x-yの散布図に

としてプロットした。

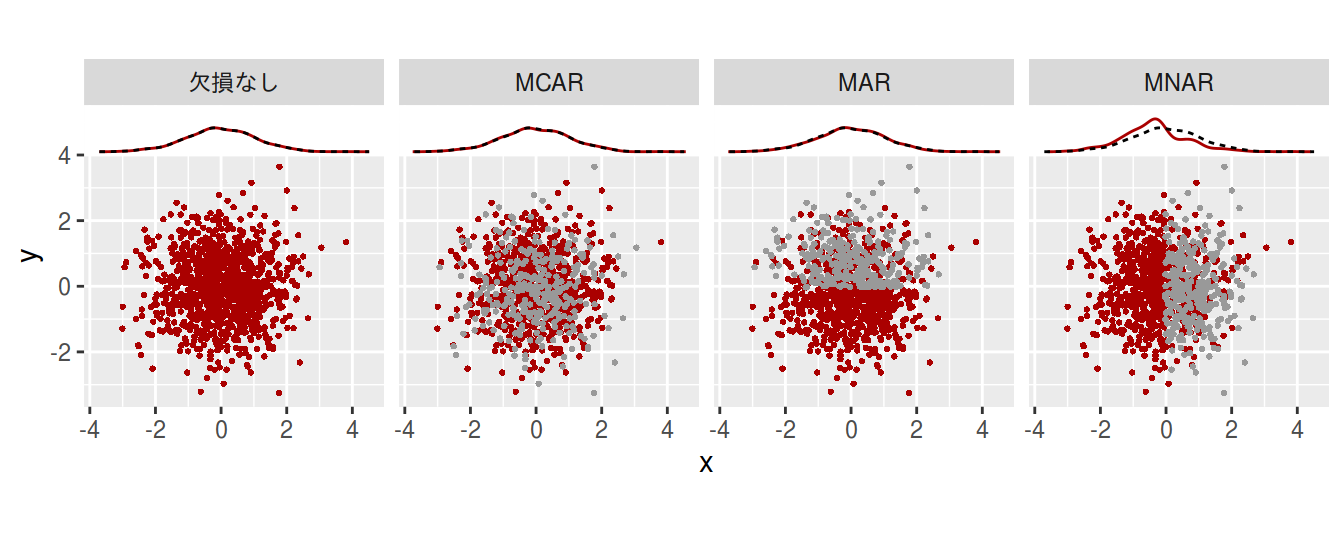
4つの図はそれぞれ

散布図の上部に描かれた線は

尚、1000点用意したデータのうち、欠損した点の数はMCAR, MAR, MNARいずれの場合も300点ずつである。

面白いのはMCARの場合でもMARの場合でもxの分布にはほとんど影響なく、yを見ない限り両者は識別不能であることだ。一方でMNARではxの分布が大きく歪むので、解析結果にバイアスが発生しやすいことに注意する必要がある。

ところで、MNARなxの欠損は x > 0 の時のみ起きると条件付けているものの、 x > 0 なデータの中からはランダムに選ばれている。 Not At Randomというのは見かけ上の問題に過ぎない。勿論、x > 0 を全損させれば、Not At Randomにもできる (ランダムに全損したと解釈することもできるが!)。

同様にMARな欠損を今回はランダムに選んだが、例えばy > 0な点を全損させてはどうだろうか。

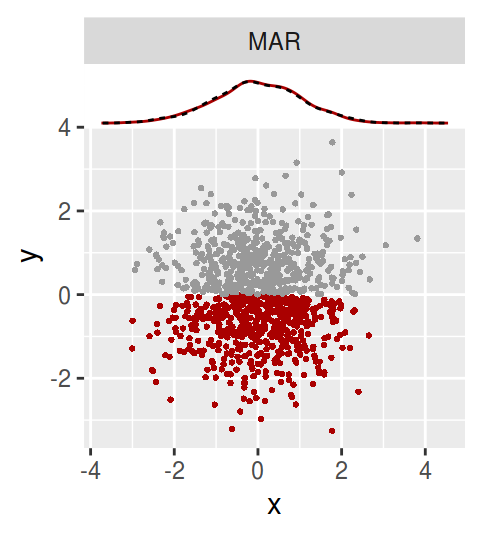
乱数を用いていないという意味ではランダムではないが、MARには違いない。 yを見ず、xにだけ注目すれば「あたかも」xはランダムに欠損している。

当記事で作成した図のソースコードはこちら。